Where do galaxies get their spin from?
A story of angular momentum,
tracer particles and data analysis
z ≥ 2: the puzzle of disk galaxies
Cite paper talking about fast rotator, disruption times, etc.
Mention Danovich, Cold flows
Simulation setup
- suite of zoom-in simulations (~6), RAMSES (Teyssier 2002)
- Δx = 35pc, Mstar = 1.1 10⁴ M☉ Mhalo=10¹² M☉
- Turbulent star formation (Kimm+17, Trebitsch+17)
- Mechanical feedback (Kimm+15)
- AGN formation with spin-regulated efficiency (Dubois+12,+14)
- 30,000,000 tracer particles (~10/cell, 0.5/star, Cadiou+19)


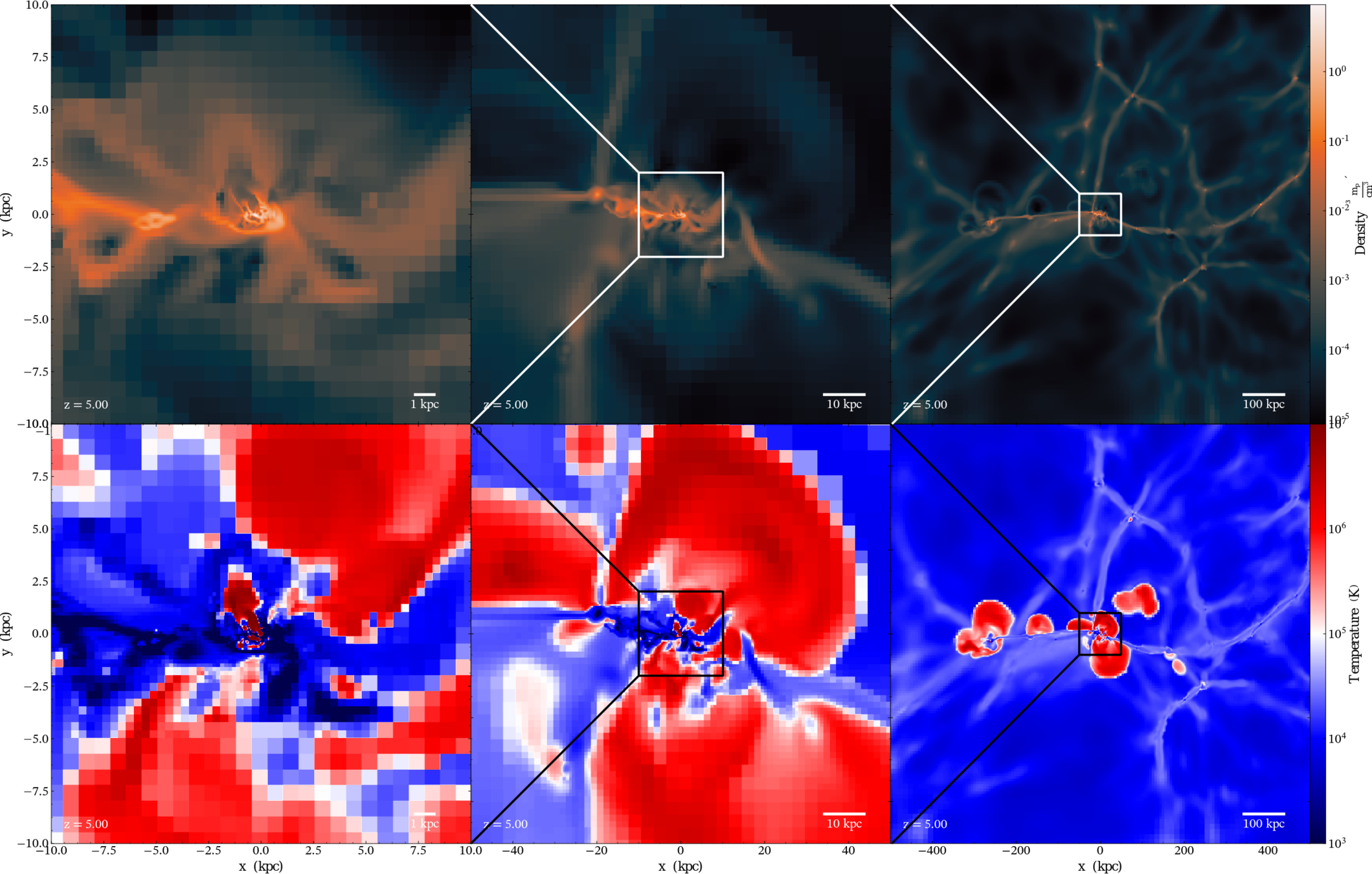
Gas density
Gas tracer density
Filamentary accretion is responsible for most of the mass and angular momentum acquisition (at z>3 ; Kereš+05, Pichon+11, Tillson+12, …)
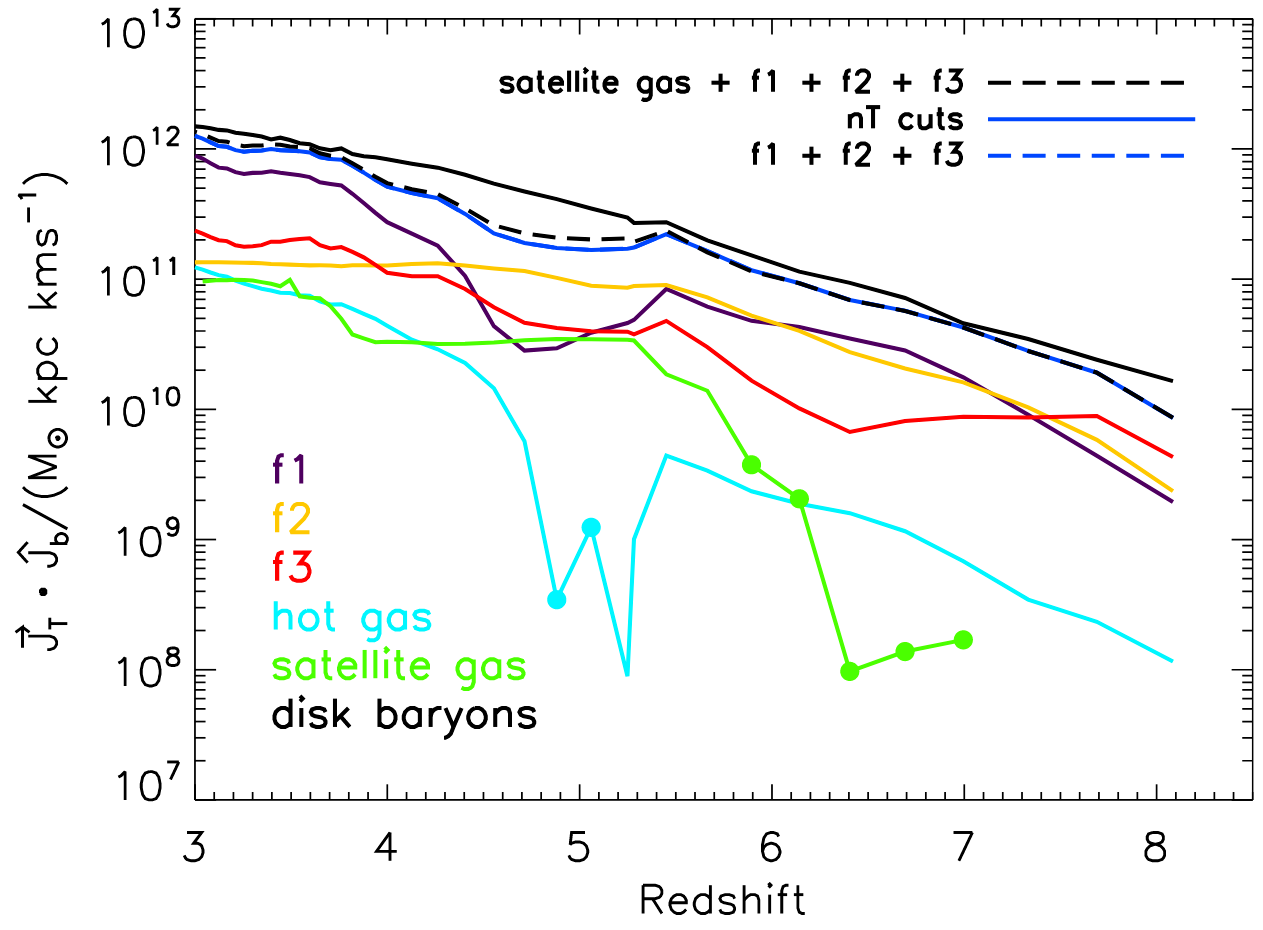
Filamentary accretion: natural "bridge" between large scale structures (cosmic web) and galaxy formation

3. Contribution to disk formation
1. AM acquisition at large scale
2. Transport along cold flows
Cold gas selection
( \( \forall t, T(t)\leq 10⁵\ \mathrm{K} \) and
\( 0.3 R_\mathrm{vir} \leq r(t) \leq 2 R_\mathrm{vir} \))
or
$$ r < 0.3 R_\mathrm{vir} \text{ or } r > 2R_\mathrm{vir} $$
Hot gas selection
$$ \exists t, T(t)> 10⁵\ \mathrm{K} \\ 0.3 R_\mathrm{vir} \leq r(t)\leq 2 R_\mathrm{vir} $$
⇒ Defined with Lagrangian history
+ removing accretion from satellites

Kinematics
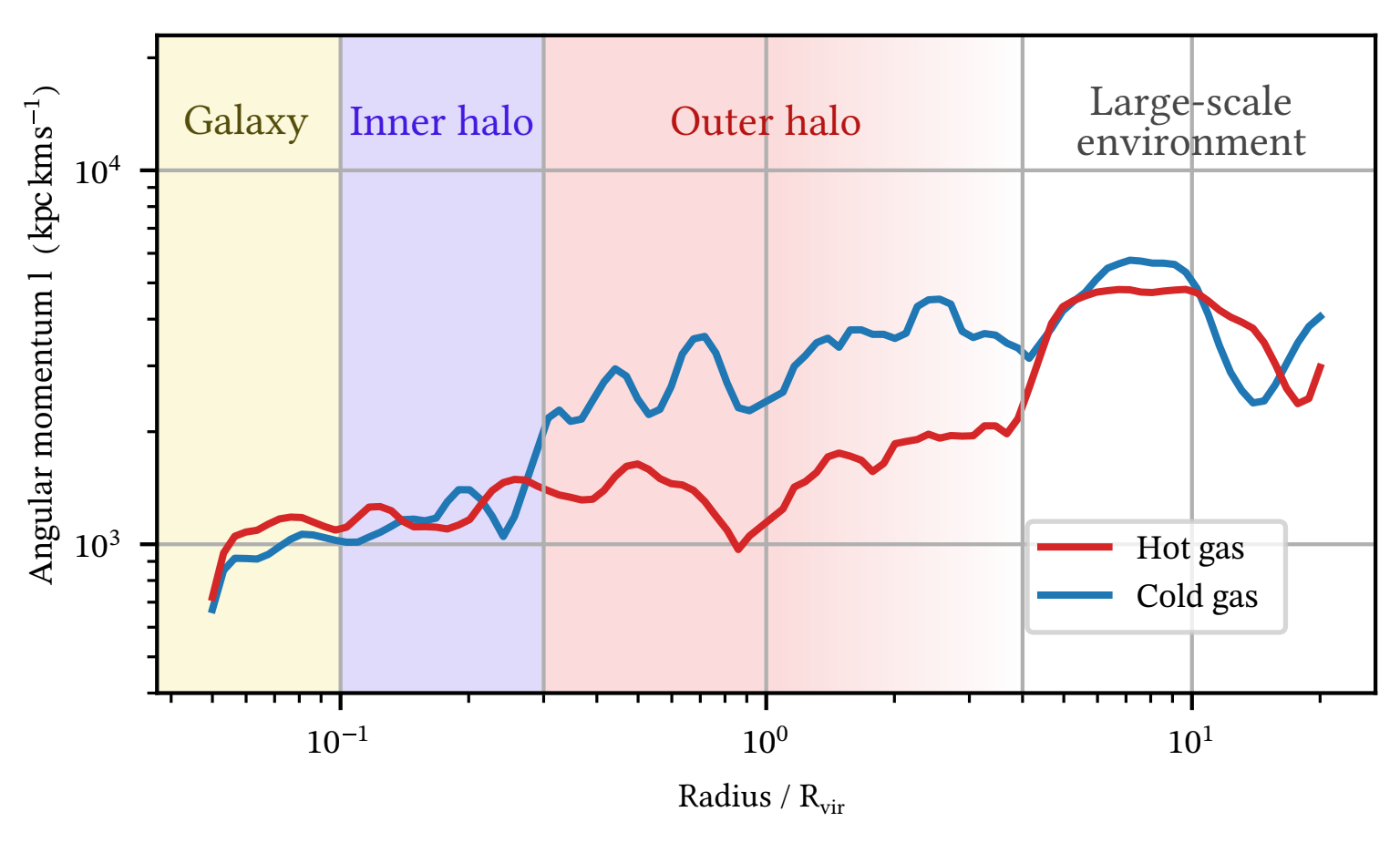
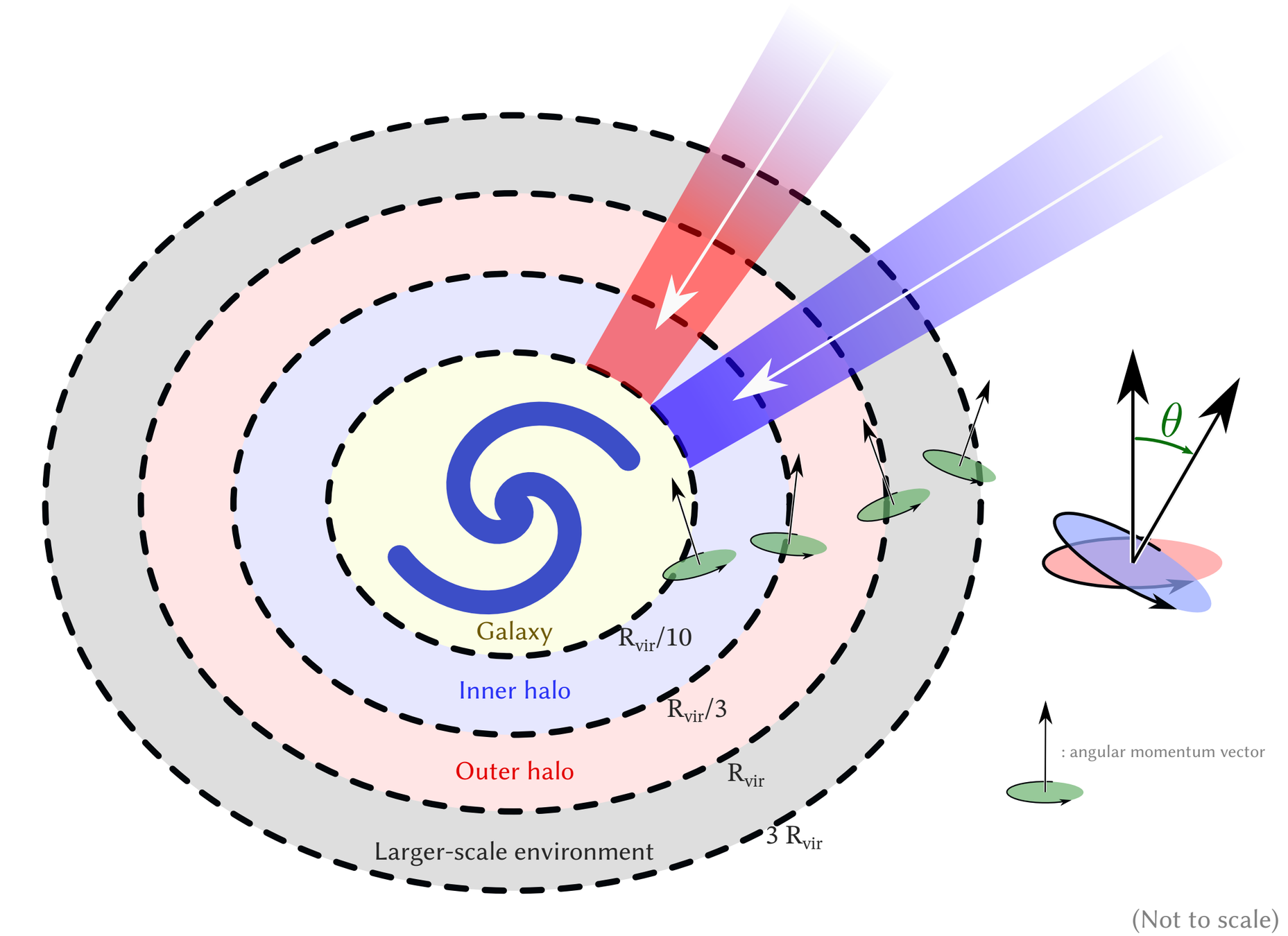
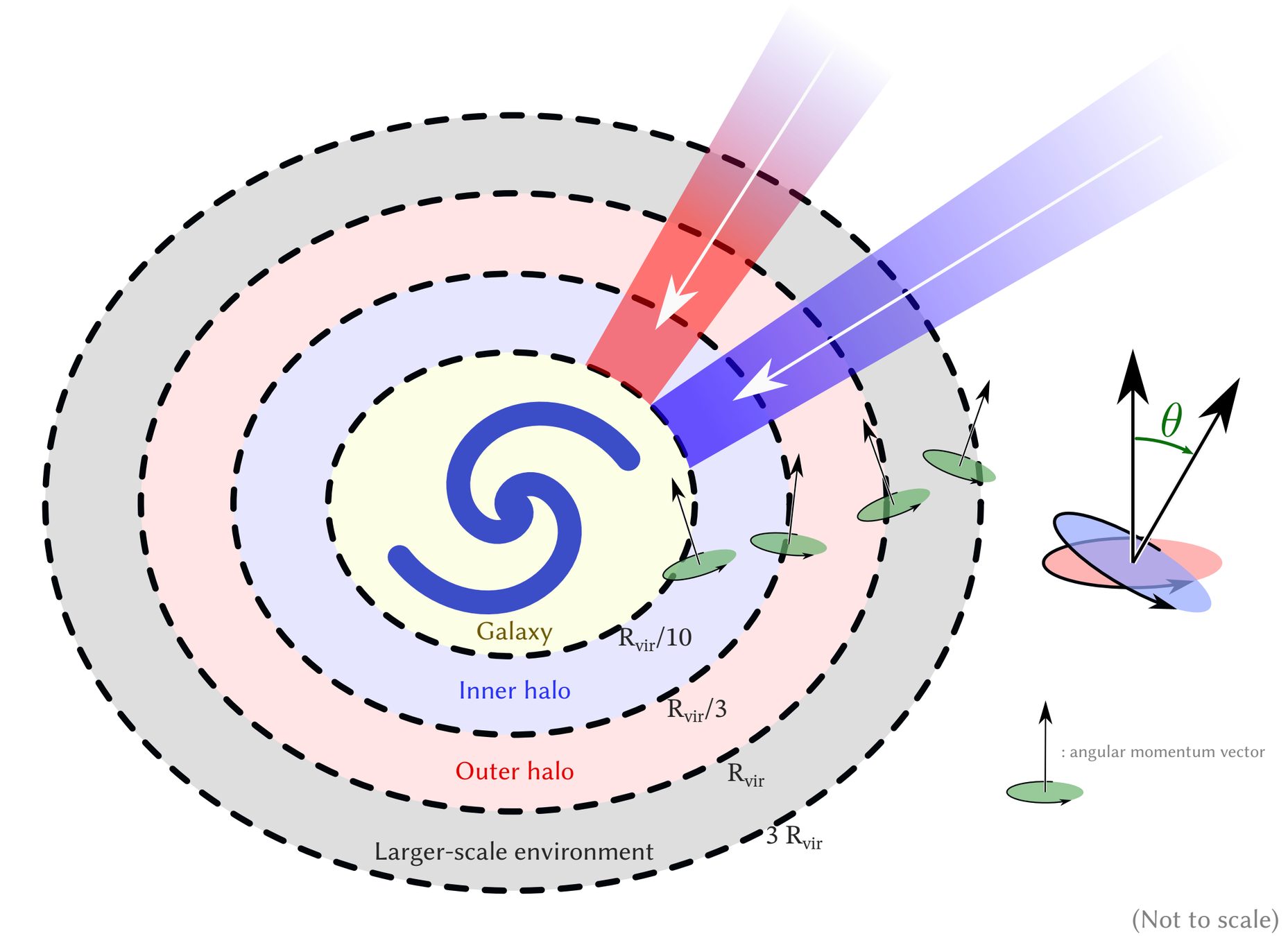
Kinematics
Cold gas: well aligned down to inner halo
Hot gas: aligned down to inner halo
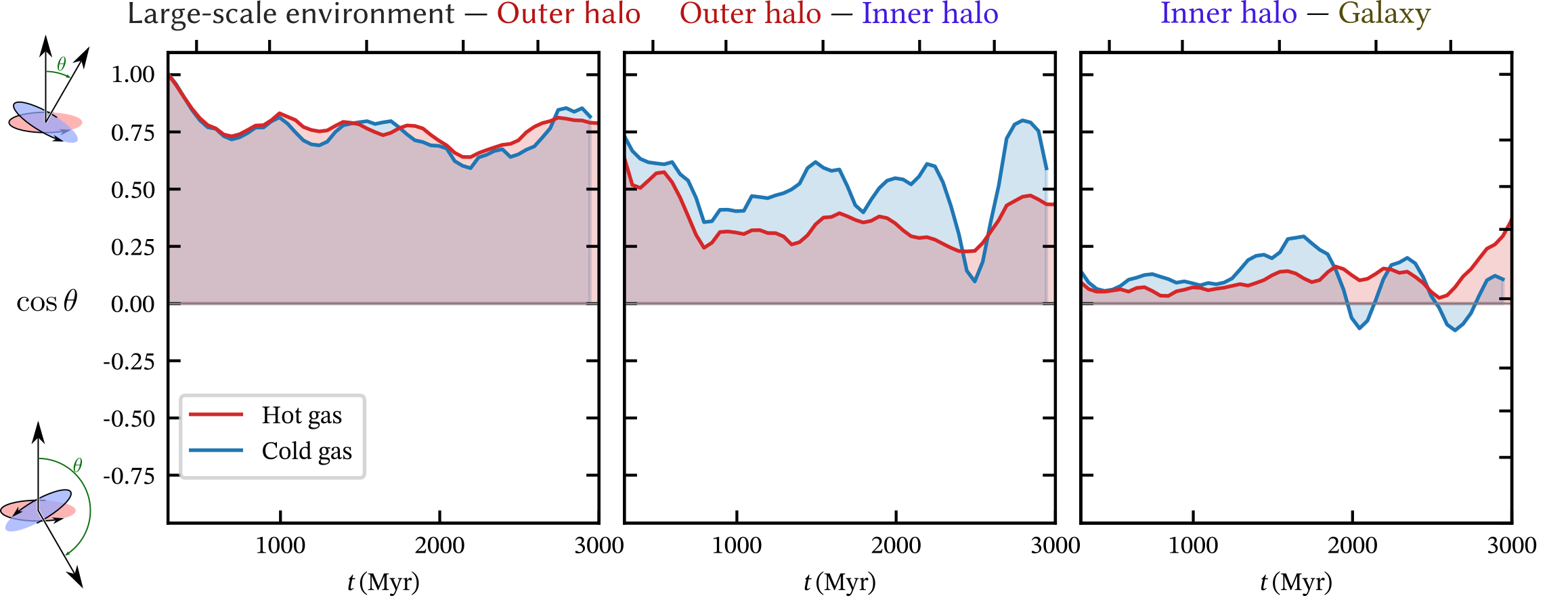
(Local) dynamics
The (Lagrangian) spAM dynamics is given by

\(\displaystyle \phantom{\frac{\mathrm{d} \mathbf{l}}{\mathrm{d} t}} + \text{gravitational torques} \)
\( \displaystyle \frac{\mathrm{d} \mathbf{l}}{\mathrm{d} t} = \textcolor{darksalmon}{\text{pressure torque}} \)
\(\displaystyle \phantom{\frac{\mathrm{d} \mathbf{l}}{\mathrm{d} t} + } \underbrace{\phantom{\text{gravitational torques}}}_{\text{\textcolor{darkgray}{DM} + \textcolor{orange}{Star} + \textcolor{deepskyblue}{Gas}}} \)
Pressure dominates the ⊥ acceleration in CGM…
locally!
Mean of ⊥ force magnitude

(Global) dynamics
Compute global torque in shell


Dynamics
Locally: pressure dominated...
esp. in the hot phase


... but globally: (DM) gravity dominated
esp. in the cold phase
What is happening?


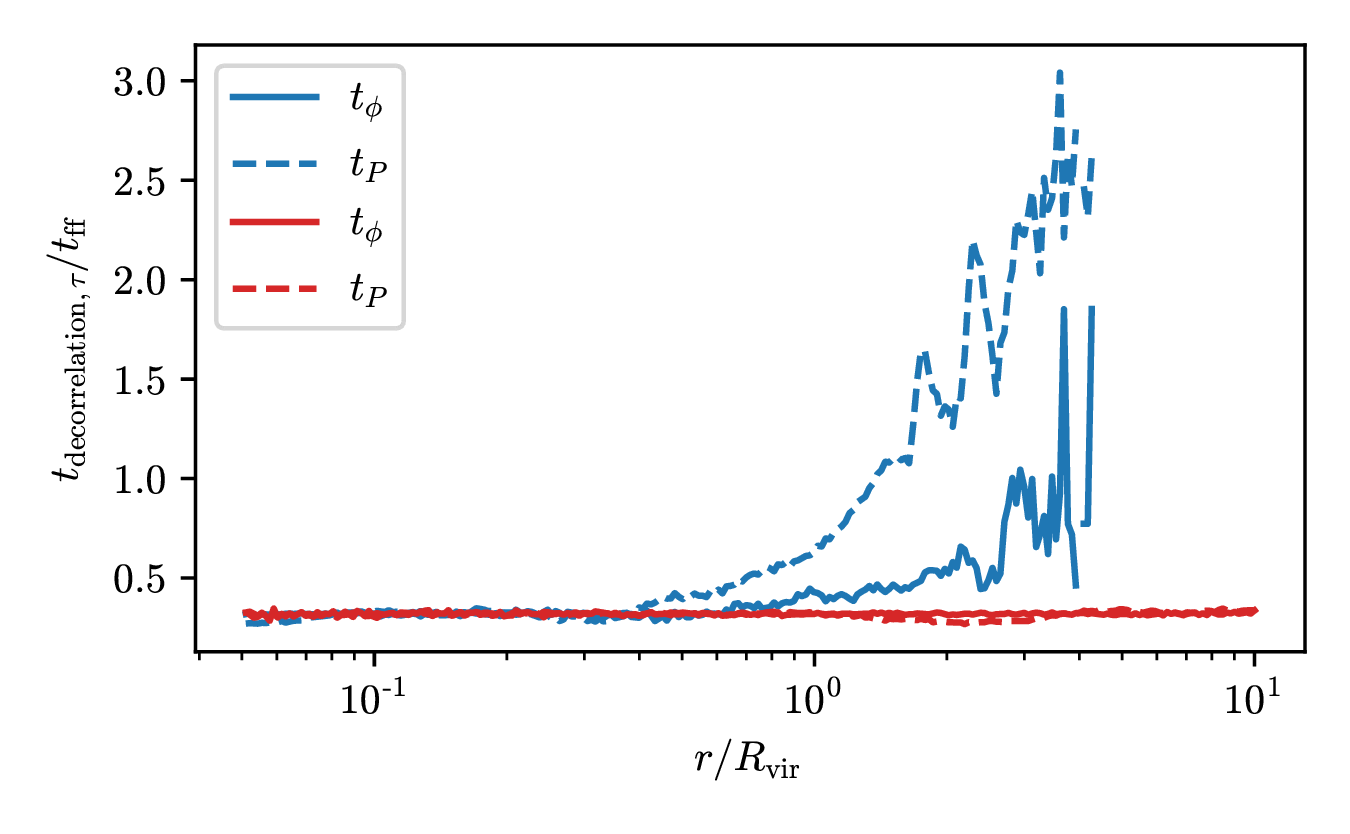
Time-coherence of torques
Compute \(t_\mathrm{decorr.}\) using Lagrangian history such that
$$ \vec{\tau}(t_\mathrm{decorr.}) \perp \vec{\tau}(0) \color{gray}\qquad\text{ (i.e. } \vec{\tau}(t_\mathrm{decorr.}) \cdot \vec{\tau}(0) = 0)$$
A/ Longer coherence in cold phase (esp. pressure)
Slow decorrelation
Fast decorrelation


Spatial-coherence of torques
Compute sum-of-norm vs norm-of-sum
$$ \dfrac{\left\| \sum_\text{neigh}\tau\right\|}{ \sum_\text{neigh}\left\| \tau\right\|} $$
B/ Pressure: \(\lambda_\mathrm{fluct.}\) is small




Spatial-coherence of torques
Compute sum-of-norm vs norm-of-sum
$$ \dfrac{\left\| \sum_\text{neigh}\tau\right\|}{ \sum_\text{neigh}\left\| \tau\right\|} $$

B/ Pressure: \(\lambda_\mathrm{fluct.}\) is small
Conclusions
Conclusions
Kinematics:
- AM transported through CGM
- orientation mostly retained down to outer disk


Dynamics:
- pressure locally dominant (esp. in hot)
- gravity globally dominant (esp. in cold)
- torques have spatial & time variations ⇒ need careful treatment


